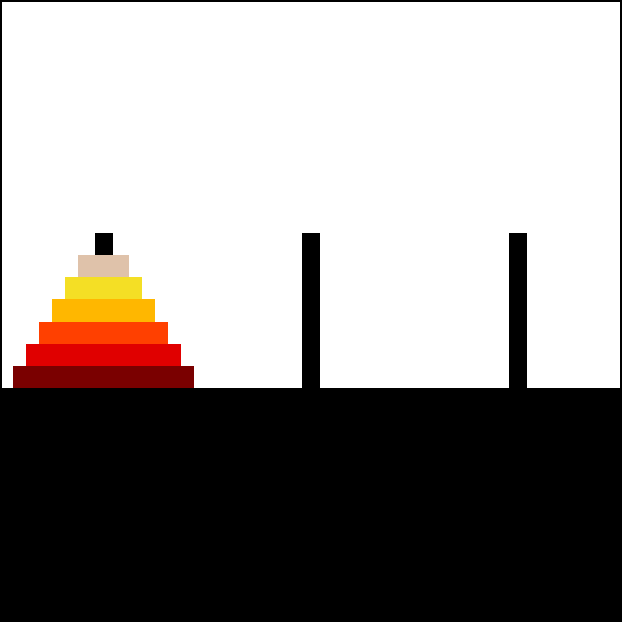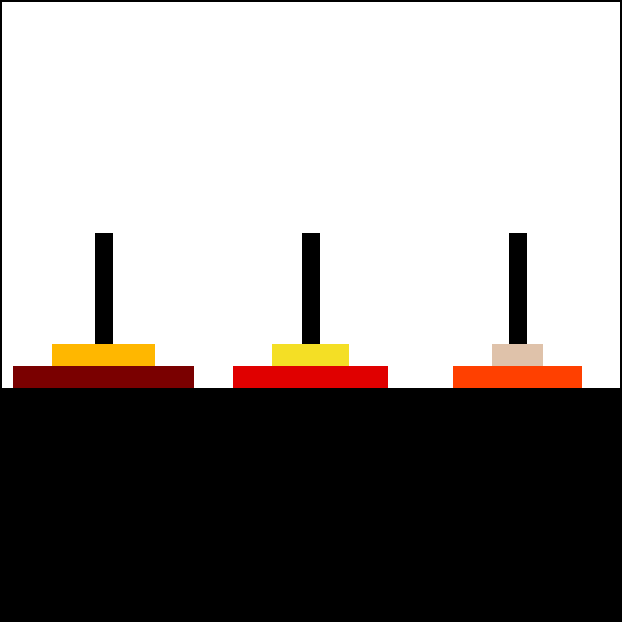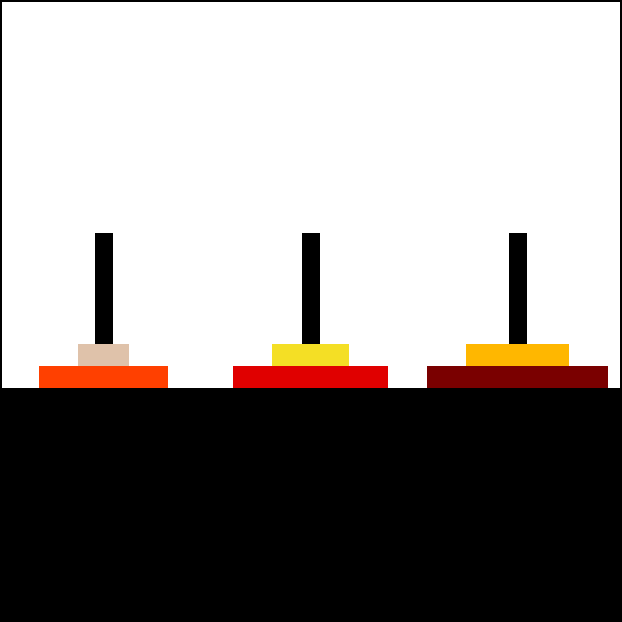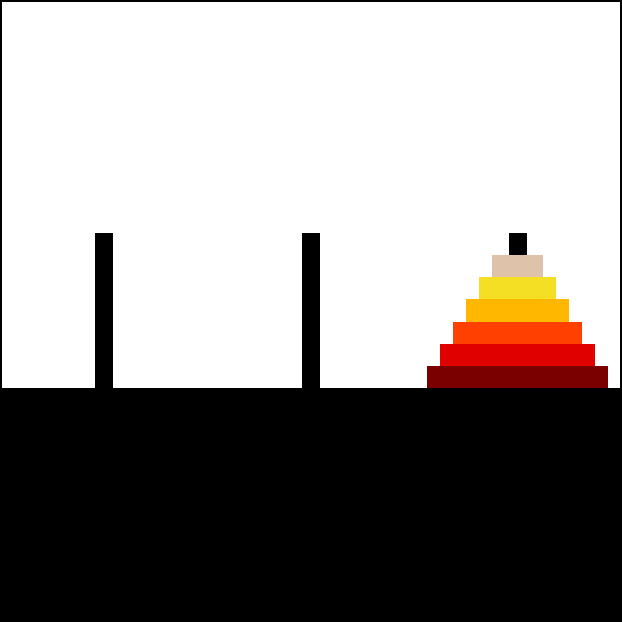Homework 3 Solutions

Solution Files

You can find the solutions in hw03.py.

Required Questions


Getting Started Videos

These videos may provide some helpful direction for tackling the coding problems on this assignment.

To see these videos, you should be logged into your berkeley.edu email.

YouTube link

Q1: Num Eights

Write a recursive function num_eights that takes a positive integer n and returns the number of times the digit 8 appears in n.

Important: Use recursion; the tests will fail if you use any assignment statements or loops. (You can define new functions, but don't put assignment statements there either.)

def num_eights(n):
    """Returns the number of times 8 appears as a digit of n.

    >>> num_eights(3)
    0
    >>> num_eights(8)
    1
    >>> num_eights(88888888)
    8
    >>> num_eights(2638)
    1
    >>> num_eights(86380)
    2
    >>> num_eights(12345)
    0
    >>> num_eights(8782089)
    3
    >>> from construct_check import check
    >>> # ban all assignment statements
    >>> check(HW_SOURCE_FILE, 'num_eights',
    ...       ['Assign', 'AnnAssign', 'AugAssign', 'NamedExpr', 'For', 'While'])
    True
    """

    if n % 10 == 8:
        return 1 + num_eights(n // 10)
    elif n < 10:
        return 0
    else:
        return num_eights(n // 10)

Use Ok to test your code:

python3 ok -q num_eights

The equivalent iterative version of this problem might look something like this:

total = 0
while n > 0:
    if n % 10 == 8:
        total = total + 1
    n = n // 10
return total

The main idea is that we check each digit for a eight. The recursive solution is similar, except that you depend on the recursive call to count the occurences of eight in the rest of the number. Then, you add that to the number of eights you see in the current digit.

Q2: Digit Distance

For a given integer, the digit distance is the sum of the absolute differences between consecutive digits. For example:

  • The digit distance of 61 is 5, as the absolute value of 6 - 1 is 5.
  • The digit distance of 71253 is 12 (abs(7-1) + abs(1-2) + abs(2-5) + abs(5-3) = 6 + 1 + 3 + 2).
  • The digit distance of 6 is 0 because there are no pairs of consecutive digits.

Write a function that determines the digit distance of a positive integer. You must use recursion or the tests will fail.

def digit_distance(n):
    """Determines the digit distance of n.

    >>> digit_distance(3)
    0
    >>> digit_distance(777) # 0 + 0
    0
    >>> digit_distance(314) # 2 + 3
    5
    >>> digit_distance(31415926535) # 2 + 3 + 3 + 4 + ... + 2
    32
    >>> digit_distance(3464660003)  # 1 + 2 + 2 + 2 + ... + 3
    16
    >>> from construct_check import check
    >>> # ban all loops
    >>> check(HW_SOURCE_FILE, 'digit_distance',
    ...       ['For', 'While'])
    True
    """

    if n < 10:
        return 0
    return abs(n % 10 - (n // 10) % 10) + digit_distance(n // 10)

# Alternate solution 1
def digit_distance_alt(n):
    def helper(prev, n):
        if n == 0:
            return 0
        dist = abs(prev - n % 10)
        return dist + helper(n % 10, n // 10)
    return helper(n % 10, n // 10)

# Alternate solution 2
def digit_distance_alt_2(n):
    def helper(dist, prev, n):
        if n == 0:
            return dist
        dist += abs(prev - n % 10)
        prev = n % 10
        n //= 10
        return helper(dist, prev, n)
    return helper(0, n % 10, n // 10)

Use Ok to test your code:

python3 ok -q digit_distance

Q3: Interleaved Sum

Write a function interleaved_sum, which takes in a number n and two one-argument functions: odd_func and even_func. It applies odd_func to every odd number and even_func to every even number from 1 to n inclusive and returns the sum.

For example, executing interleaved_sum(5, lambda x: x, lambda x: x * x) returns 1 + 2*2 + 3 + 4*4 + 5 = 29.

Important: Implement this function without using any loops or directly testing if a number is odd or even (no using %). Instead of directly checking whether a number is even or odd, start with 1, which you know is an odd number.

Hint: Introduce an inner helper function that takes an odd number k and computes an interleaved sum from k to n (including n).

def interleaved_sum(n, odd_func, even_func):
    """Compute the sum odd_func(1) + even_func(2) + odd_func(3) + ..., up
    to n.

    >>> identity = lambda x: x
    >>> square = lambda x: x * x
    >>> triple = lambda x: x * 3
    >>> interleaved_sum(5, identity, square) # 1   + 2*2 + 3   + 4*4 + 5
    29
    >>> interleaved_sum(5, square, identity) # 1*1 + 2   + 3*3 + 4   + 5*5
    41
    >>> interleaved_sum(4, triple, square)   # 1*3 + 2*2 + 3*3 + 4*4
    32
    >>> interleaved_sum(4, square, triple)   # 1*1 + 2*3 + 3*3 + 4*3
    28
    >>> from construct_check import check
    >>> check(HW_SOURCE_FILE, 'interleaved_sum', ['While', 'For', 'Mod']) # ban loops and %
    True
    >>> check(HW_SOURCE_FILE, 'interleaved_sum', ['BitAnd', 'BitOr', 'BitXor']) # ban bitwise operators, don't worry about these if you don't know what they are
    True
    """

    def sum_from(k):
        if k > n:
            return 0
        elif k == n:
            return odd_func(k)
        else:
            return odd_func(k) + even_func(k+1) + sum_from(k + 2)
    return sum_from(1)

Use Ok to test your code:

python3 ok -q interleaved_sum

Q4: Count Dollars

Given a positive integer total, a set of dollar bills makes change for total if the sum of the values of the dollar bills is total. Here we will use standard US dollar bill values: 1, 5, 10, 20, 50, and 100. For example, the following sets make change for 15:

  • 15 1-dollar bills
  • 10 1-dollar, 1 5-dollar bills
  • 5 1-dollar, 2 5-dollar bills
  • 5 1-dollar, 1 10-dollar bills
  • 3 5-dollar bills
  • 1 5-dollar, 1 10-dollar bills

Thus, there are 6 ways to make change for 15. Write a recursive function count_dollars that takes a positive integer total and returns the number of ways to make change for total using 1, 5, 10, 20, 50, and 100 dollar bills.

Use next_smaller_dollar in your solution: next_smaller_dollar will return the next smaller dollar bill value from the input (e.g. next_smaller_dollar(5) is 1). The function will return None if the next dollar bill value does not exist.

Important: Use recursion; the tests will fail if you use loops.

Hint: Refer to the implementation of count_partitions for an example of how to count the ways to sum up to a final value with smaller parts. If you need to keep track of more than one value across recursive calls, consider writing a helper function.

def next_smaller_dollar(bill):
    """Returns the next smaller bill in order."""
    if bill == 100:
        return 50
    if bill == 50:
        return 20
    if bill == 20:
        return 10
    elif bill == 10:
        return 5
    elif bill == 5:
        return 1

def count_dollars(total):
    """Return the number of ways to make change.

    >>> count_dollars(15)  # 15 $1 bills, 10 $1 & 1 $5 bills, ... 1 $5 & 1 $10 bills
    6
    >>> count_dollars(10)  # 10 $1 bills, 5 $1 & 1 $5 bills, 2 $5 bills, 10 $1 bills
    4
    >>> count_dollars(20)  # 20 $1 bills, 15 $1 & $5 bills, ... 1 $20 bill
    10
    >>> count_dollars(45)  # How many ways to make change for 45 dollars?
    44
    >>> count_dollars(100) # How many ways to make change for 100 dollars?
    344
    >>> count_dollars(200) # How many ways to make change for 200 dollars?
    3274
    >>> from construct_check import check
    >>> # ban iteration
    >>> check(HW_SOURCE_FILE, 'count_dollars', ['While', 'For'])
    True
    """

    def constrained_count(total, largest_bill):
        if total == 0:
            return 1
        if total < 0:
            return 0
        if largest_bill == None:
            return 0
        without_dollar_bill = constrained_count(total, next_smaller_dollar(largest_bill))
        with_dollar_bill = constrained_count(total - largest_bill, largest_bill)
        return without_dollar_bill + with_dollar_bill
    return constrained_count(total, 100)

Use Ok to test your code:

python3 ok -q count_dollars

This is remarkably similar to the count_partitions problem, with a few minor differences:

  • A maximum partition size is not given, so we need to create a helper function that takes in two arguments: current total and dollar bill value.
  • Partition size is not linear. To get the next partition you need to call next_smaller_dollar.

Check Your Score Locally

You can locally check your score on each question of this assignment by running

python3 ok --score

This does NOT submit the assignment! When you are satisfied with your score, submit the assignment to Gradescope to receive credit for it.

Submit Assignment

Submit this assignment by uploading any files you've edited to the appropriate Gradescope assignment. Lab 00 has detailed instructions.

Optional Questions

These questions are optional. If you don't complete them, you will still receive credit for this assignment. They are great practice, so do them anyway!

Q5: Count Dollars Upward

Write a recursive function count_dollars_upward that is just like count_dollars except it uses next_larger_dollar, which returns the next larger dollar bill value from the input (e.g. next_larger_dollar(5) is 10). The function will return None if the next dollar bill value does not exist.

Important: Use recursion; the tests will fail if you use loops.

def next_larger_dollar(bill):
    """Returns the next larger bill in order."""
    if bill == 1:
        return 5
    elif bill == 5:
        return 10
    elif bill == 10:
        return 20
    elif bill == 20:
        return 50
    elif bill == 50:
        return 100

def count_dollars_upward(total):
    """Return the number of ways to make change using bills.

    >>> count_dollars_upward(15)  # 15 $1 bills, 10 $1 & 1 $5 bills, ... 1 $5 & 1 $10 bills
    6
    >>> count_dollars_upward(10)  # 10 $1 bills, 5 $1 & 1 $5 bills, 2 $5 bills, 10 $1 bills
    4
    >>> count_dollars_upward(20)  # 20 $1 bills, 15 $1 & $5 bills, ... 1 $20 bill
    10
    >>> count_dollars_upward(45)  # How many ways to make change for 45 dollars?
    44
    >>> count_dollars_upward(100) # How many ways to make change for 100 dollars?
    344
    >>> count_dollars_upward(200) # How many ways to make change for 200 dollars?
    3274
    >>> from construct_check import check
    >>> # ban iteration
    >>> check(HW_SOURCE_FILE, 'count_dollars_upward', ['While', 'For'])
    True
    """

    def constrained_count(total, smallest_bill):
        if total == 0:
            return 1
        if total < 0:
            return 0
        if smallest_bill == None:
            return 0
        without_dollar_bill = constrained_count(total, next_larger_dollar(smallest_bill))
        with_dollar_bill = constrained_count(total - smallest_bill, smallest_bill)
        return without_dollar_bill + with_dollar_bill
    return constrained_count(total, 1)

Use Ok to test your code:

python3 ok -q count_dollars_upward

This is remarkably similar to the count_partitions problem, with a few minor differences:

  • A maximum partition size is not given, so we need to create a helper function that takes in two arguments: current total and dollar bill value.
  • Partition size is not linear. To get the next partition you need to call next_larger_dollar.

Exam Practice

Homework assignments will also contain prior exam-level questions for you to take a look at. These questions have no submission component; feel free to attempt them if you'd like a challenge!

  1. Fall 2017 MT1 Q4a: Digital
  2. Fall 2019 Final Q6b: Palindromes

Just For Fun Questions

The questions below are out of scope for 61A. You can try them if you want an extra challenge, but they're just puzzles that are not required for the course. Almost all students will skip them, and that's fine. We will not be prioritizing support for these questions on Ed or during Office Hours.

Q6: Towers of Hanoi

A classic puzzle called the Towers of Hanoi is a game that consists of three rods, and a number of disks of different sizes which can slide onto any rod. The puzzle starts with n disks in a neat stack in ascending order of size on a start rod, the smallest at the top, forming a conical shape. Towers of Hanoi The objective of the puzzle is to move the entire stack to an end rod, obeying the following rules:
  • Only one disk may be moved at a time.
  • Each move consists of taking the top (smallest) disk from one of the rods and sliding it onto another rod, on top of the other disks that may already be present on that rod.
  • No disk may be placed on top of a smaller disk.
Complete the definition of move_stack, which prints out the steps required to move n disks from the start rod to the end rod without violating the rules. The provided print_move function will print out the step to move a single disk from the given origin to the given destination.

Hint: Draw out a few games with various n on a piece of paper and try to find a pattern of disk movements that applies to any n. In your solution, take the recursive leap of faith whenever you need to move any amount of disks less than n from one rod to another. If you need more help, see the following hints.

See the following animation of the Towers of Hanoi, found on Wikimedia by user Trixx.


The strategy used in Towers of Hanoi is to move all but the bottom disc to the second peg, then moving the bottom disc to the third peg, then moving all but the second disc from the second to the third peg.


One thing you don't need to worry about is collecting all the steps. print effectively "collects" all the results in the terminal as long as you make sure that the moves are printed in order.

def print_move(origin, destination):
    """Print instructions to move a disk."""
    print("Move the top disk from rod", origin, "to rod", destination)

def move_stack(n, start, end):
    """Print the moves required to move n disks on the start pole to the end
    pole without violating the rules of Towers of Hanoi.

    n -- number of disks
    start -- a pole position, either 1, 2, or 3
    end -- a pole position, either 1, 2, or 3

    There are exactly three poles, and start and end must be different. Assume
    that the start pole has at least n disks of increasing size, and the end
    pole is either empty or has a top disk larger than the top n start disks.

    >>> move_stack(1, 1, 3)
    Move the top disk from rod 1 to rod 3
    >>> move_stack(2, 1, 3)
    Move the top disk from rod 1 to rod 2
    Move the top disk from rod 1 to rod 3
    Move the top disk from rod 2 to rod 3
    >>> move_stack(3, 1, 3)
    Move the top disk from rod 1 to rod 3
    Move the top disk from rod 1 to rod 2
    Move the top disk from rod 3 to rod 2
    Move the top disk from rod 1 to rod 3
    Move the top disk from rod 2 to rod 1
    Move the top disk from rod 2 to rod 3
    Move the top disk from rod 1 to rod 3
    """
    assert 1 <= start <= 3 and 1 <= end <= 3 and start != end, "Bad start/end"

    if n == 1:
        print_move(start, end)
    else:
        other = 6 - start - end
        move_stack(n-1, start, other)
        print_move(start, end)
        move_stack(n-1, other, end)

Use Ok to test your code:

python3 ok -q move_stack

To solve the Towers of Hanoi problem for n disks, we need to do three steps:

  1. Move everything but the last disk (n-1 disks) to someplace in the middle (not the start nor the end rod).
  2. Move the last disk (a single disk) to the end rod. This must occur after step 1 (we have to move everything above it away first)!
  3. Move everything but the last disk (the disks from step 1) from the middle on top of the end rod.

We take advantage of the fact that the recursive function move_stack is guaranteed to move n disks from start to end while obeying the rules of Towers of Hanoi. The only thing that remains is to make sure that we have set up the playing board to make that possible.

Since we move a disk to end rod, we run the risk of move_stack doing an improper move (big disk on top of small disk). But since we're moving the biggest disk possible, nothing in the n-1 disks above that is bigger. Therefore, even though we do not explicitly state the Towers of Hanoi constraints, we can still carry out the correct steps.

Video walkthrough:

YouTube link

Q7: Anonymous Factorial

This question demonstrates that it's possible to write recursive functions without assigning them a name in the global frame.

The recursive factorial function can be written as a single expression by using a conditional expression.

>>> fact = lambda n: 1 if n == 1 else mul(n, fact(sub(n, 1)))
>>> fact(5)
120

However, this implementation relies on the fact (no pun intended) that fact has a name, to which we refer in the body of fact. To write a recursive function, we have always given it a name using a def or assignment statement so that we can refer to the function within its own body. In this question, your job is to define fact recursively without giving it a name!

Write an expression that computes n factorial using only call expressions, conditional expressions, and lambda expressions (no assignment or def statements).

Note: You are not allowed to use make_anonymous_factorial in your return expression.

The sub and mul functions from the operator module are the only built-in functions required to solve this problem.

from operator import sub, mul

def make_anonymous_factorial():
    """Return the value of an expression that computes factorial.

    >>> make_anonymous_factorial()(5)
    120
    >>> from construct_check import check
    >>> # ban any assignments or recursion
    >>> check(HW_SOURCE_FILE, 'make_anonymous_factorial',
    ...     ['Assign', 'AnnAssign', 'AugAssign', 'NamedExpr', 'FunctionDef', 'Recursion'])
    True
    """

    return (lambda f: lambda k: f(f, k))(lambda f, k: k if k == 1 else mul(k, f(f, sub(k, 1))))
    # Alternate solution:
    return (lambda f: f(f))(lambda f: lambda x: 1 if x == 0 else x * f(f)(x - 1))

Use Ok to test your code:

python3 ok -q make_anonymous_factorial