Homework 8 Solutions

hw08.zip

Solution Files

You can find the solutions in hw08.scm.

The 61A Scheme interpreter is included in each Scheme assignment. To start it, type python3 scheme in a terminal. To load a Scheme file called f.scm, type python3 scheme -i f.scm. To exit the Scheme interpreter, type (exit).

Scheme Editor

All Scheme assignments include a web-based editor that makes it easy to run ok tests and visualize environments. Type python3 editor in a terminal, and the editor will open in a browser window (at http://127.0.0.1:31415/). To stop running the editor and return to the command line, type Ctrl-C in the terminal where you started the editor.

The Run button loads the current assignment's .scm file and opens a Scheme interpreter, allowing you to try evaluating different Scheme expressions.

The Test button runs all ok tests for the assignment. Click View Case for a failed test, then click Debug to step through its evaluation.

Recommended VS Code Extensions

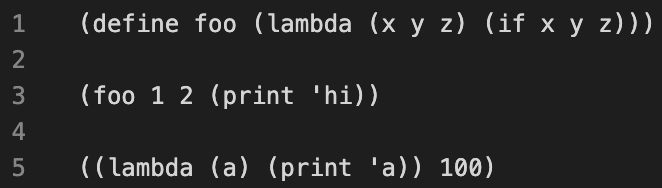
If you choose to use VS Code as your text editor (instead of the web-based editor), install the vscode-scheme extension so that parentheses are highlighted.

Before:

After:

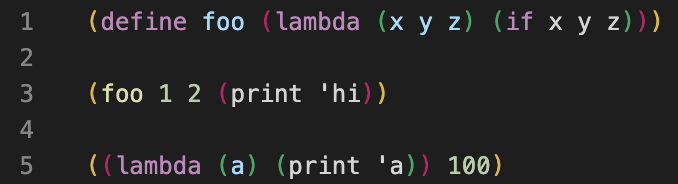
In addition, the 61a-bot (installation instructions) VS Code extension is available for Scheme homeworks. The bot is also integrated into ok.

Required Questions

Getting Started Videos

These videos may provide some helpful direction for tackling the coding problems on this assignment.

To see these videos, you should be logged into your berkeley.edu email.

YouTube link

Q1: Ascending

Implement a procedure called ascending?, which takes a list of numbers s and returns True if the numbers are in non-descending order, and False otherwise.

A list of numbers is non-descending if each element after the first is greater than or equal to the previous element. For example...

(1 2 3 3 4) is non-descending.
(1 2 3 3 2) is not.

Hint: The built-in null? procedure returns whether its argument is nil.

Note: The question mark in ascending? is just part of the procedure name and has no special meaning in terms of Scheme syntax. It is a common practice in Scheme to name procedures with a question mark at the end if it returns a boolean value.

(define (ascending? s)
  (if (or (null? s) (null? (cdr s)))
      #t
      (and (<= (car s) (car (cdr s))) (ascending? (cdr s))))
)

We approach this much like a standard Python linked list problem.

Base case: when s has zero or one items, it is non-descending.
For the recursive case, we check that the second element is greater or equal to the first and that the rest is non-descending.

Use Ok to unlock and test your code:

python3 ok -q ascending -u
python3 ok -q ascending

Q2: My Filter

Write a procedure my-filter, which takes a predicate pred and a list s, and returns a new list containing only elements of the list that satisfy the predicate. The output should contain the elements in the same order that they appeared in the original list.

Note: Make sure that you are not just calling the built-in filter function in Scheme - we are asking you to re-implement this!

(define (my-filter pred s)
  (cond ((null? s) '())
        ((pred (car s)) (cons (car s) (my-filter pred (cdr s))))
        (else (my-filter pred (cdr s))))
)

YouTube link

The approach for this problem is to call pred on each element, which we can access with car.

If a given element satisfies pred, then it "passes" the filter and can be included in our new list.
If the element does not, then we simply return the recursive call because we should not include the element.

Use Ok to unlock and test your code:

python3 ok -q filter -u
python3 ok -q filter

Q3: Interleave

Implement the function interleave, which takes two lists lst1 and lst2 as arguments. interleave should return a new list that interleaves the elements of the two lists. (In other words, the resulting list should contain elements alternating between lst1 and lst2, starting at lst1).

If one of the input lists to interleave is shorter than the other, then interleave should alternate elements from both lists until one list has no more elements, and then the remaining elements from the longer list should be added to the end of the new list.

(define (interleave lst1 lst2)
  (if (or (null? lst1) (null? lst2))
      (append lst1 lst2)
      (cons (car lst1)
            (cons (car lst2)
                  (interleave (cdr lst1) (cdr lst2)))))
)
; Alternate Solution
(define (interleave lst1 lst2) 
  (cond 
    ((null? lst1) lst2)
    ((null? lst2) lst1)
    (else (cons (car lst1) (interleave lst2 (cdr lst1))))
  )
)

The base cases for both solutions (which are equivalent), follow directly from the spec. That is, if we run out of elements in one list, then we should simply append the remaining elements from the longer list.

The first solution constructs the interleaved list two elements at a time, by cons-ing together the first two elements of each list alongside the result of recursively calling interleave on the cdr's of both lists.

The second solution constructs the interleaved list one element at a time by swapping which list is passed in for lst1. Thus, we can then grab elements from only lst1 to construct the list.

Use Ok to unlock and test your code:

python3 ok -q interleave -u
python3 ok -q interleave

Q4: No Repeats

Implement no-repeats, which takes a list of numbers s. It returns a list that has all of the unique elements of s in the order that they first appear, but no repeats.

For example, (no-repeats (list 5 4 5 4 2 2)) evaluates to (5 4 2).

Hint: You may find it helpful to use filter with a lambda procedure to filter out repeats. To test if two numbers a and b are not equal, use (not (= a b)).

(define (no-repeats s)
  (if (null? s) s
    (cons (car s)
      (no-repeats (filter (lambda (x) (not (= (car s) x))) (cdr s)))))
)

For the base case, if the input list is empty, then we do nothing and return the empty list.

Otherwise, we may attempt to proceed with the intuition that removing repeats would require us to keep track of what elements we have already "seen". However, this would require a helper to keep track of seen elements. Furthermore, Scheme does not have a built-in containment predicate analog to Python's in keyword.

Thus, we realize that we can instead remove all repeats of an element while iterating through our list. The idea is that as we iterate through an element of the list, we simultaneously remove all other instances of that element from the rest of the list. This ensures that there is only one instance of that element in the list. We achieve this by applying a filter onto the rest of the list.

Use Ok to test your code:

python3 ok -q no_repeats

Submit

Submit this assignment by uploading any files you've edited to the appropriate Gradescope assignment. Lab 00 has detailed instructions.

In addition, all students who are not in the mega lab must complete this attendance form. Submit this form each week, whether you attend lab or missed it for a good reason. The attendance form is not required for mega section students.

Exam Practice

The following are some Scheme List exam problems from previous semesters that you may find useful as additional exam practice.