Discussion 8: Scheme, Scheme Lists
Scheme
define form is used to assign values to symbols. It has the following syntax:
(define <symbol> <expression>)scm> (define pi (+ 3 0.14))
pi
scm> pi
3.14To evaluate the define expression:
- Evaluate the final sub-expression (
<expression>), which in this case evaluates to3.14. - Bind that value to the symbol (
symbol), which in this case ispi. - Return the symbol.
The define form can also define new procedures, described in the "Defining Functions" section.
The define form can create a procedure and give it a name:
(define (<symbol> <param1> <param2> ...) <body>)For example, this is how we would define the double procedure:
scm> (define (double x) (* x 2))
double
scm> (double 3)
6Here's an example with three arguments:
scm> (define (add-then-mul x y z)
(* (+ x y) z))
scm> (add-then-mul 3 4 5)
35When a define expression is evaluated, the following occurs:
- Create a procedure with the given parameters and
<body>. - Bind the procedure to the
<symbol>in the current frame. - Return the
<symbol>.
The following two expressions are equivalent:
scm> (define add (lambda (x y) (+ x y)))
add
scm> (define (add x y) (+ x y))
addAtomic expressions (also called atoms) are expressions without sub-expressions, such as numbers, boolean values, and symbols.
scm> 1234 ; integer
1234
scm> 123.4 ; real number
123.4
scm> #f ; the Scheme equivalent of False in Python
#fA Scheme symbol is equivalent to a Python name. A symbol evaluates to the value bound to that symbol in the current environment. (They are called symbols rather than names because they include + and other arithmetic symbols.)
scm> quotient ; A symbol bound to a built-in procedure
#[quotient]
scm> + ; A symbol bound to a built-in procedure
#[+]In Scheme, all values except #f (equivalent to False in Python) are true
values (unlike Python, which has other false values, such as 0).
scm> #t
#t
scm> #f
#fThe if special form evaluates one of two expressions based on a predicate.
(if <predicate> <if-true> <if-false>)The rules for evaluating an if special form expression are as follows:
- Evaluate the
<predicate>. - If the
<predicate>evaluates to a true value (anything but#f), evaluate and return the value of the<if-true>expression. Otherwise, evaluate and return the value of the<if-false>expression.
For example, this expression does not error and evaluates to 5, even though the
sub-expression (/ 1 (- x 3)) would error if evaluated.
scm> (define x 3)
x
scm> (if (> (- x 3) 0) (/ 1 (- x 3)) (+ x 2))
5The <if-false> expression is optional.
scm> (if (= x 3) (print x))
3Let's compare a Scheme if expression with a Python if statement:
- In Scheme:
(if (> x 3) 1 2)- In Python:
if x > 3:
1
else:
2The Scheme if expression evaluates to a number (either 1 or 2, depending on
x). The Python statement does not evaluate to anything, and so the 1 and 2
cannot be used or accessed.
Another difference between the two is that it's possible to add more lines of
code into the suites of the Python if statement, while a Scheme if
expression expects just a single expression in each of the <if-true> and
<if-false> positions.
One final difference is that in Scheme, you cannot write elif clauses.
Q1: Perfect Fit
Definition: A perfect square is k*k for some integer k.
Implement fit, which takes non-negative integers total and n. It returns
whether there are n different positive perfect squares that sum to
total.
Important: Don't use the Scheme interpreter to tell you whether you've implemented it correctly. Discuss! On the final exam, you won't have an interpreter.
Your Answer Run in 61A Code ; Return whether there are n perfect squares with no repeats that sum to total
(define (fit total n)
(define (f total n k)
(if (and (= n 0) (= total 0))
#t
(if (< total (* k k))
#f
(or (f total n (+ k 1)) (f (- total (* k k)) (- n 1) (+ k 1)))
)))
(f total n 1))
(expect (fit 10 2) #t) ; 1*1 + 3*3
(expect (fit 9 1) #t) ; 3*3
(expect (fit 9 2) #f) ;
(expect (fit 9 3) #f) ; 1*1 + 2*2 + 2*2 doesn't count because of repeated 2*2
(expect (fit 25 1) #t) ; 5*5
(expect (fit 25 2) #t) ; 3*3 + 4*4Use the (or _ _) special form to combine two recursive calls: one that uses
k*k in the sum and one that does not. The first should subtract k*k from
total and subtract 1 from n; the other should leaves total and n
unchanged.
Q2: Interleave
Implement the function interleave, which takes two lists lst1 and lst2 as
arguments. interleave should return a list that interleaves the elements
of the two lists. (In other words, the resulting list should contain elements
alternating between lst1 and lst2, starting at lst1).
If one of the input lists to interleave is shorter than the other, then
interleave should alternate elements from both lists until one list has no
more elements, and then the remaining elements from the longer list should be
added to the end of the new list. If lst1 is empty, you may simply return
lst2 and vice versa.
(define (interleave lst1 lst2)
(if (or (null? lst1) (null? lst2))
(append lst1 lst2)
(cons (car lst1)
(cons (car lst2)
(interleave (cdr lst1) (cdr lst2)))))
; Alternate Solution
(cond
((null? lst1) lst2)
((null? lst2) lst1)
(else (cons (car lst1) (interleave lst2 (cdr lst1))))
)
)The base cases for both solutions (which are equivalent), follow directly from the spec. That is, if we run out of elements in one list, then we should simply append the remaining elements from the longer list.
The first solution constructs the interleaved list two elements at a time, by cons-ing together the first
two elements of each list alongside the result of recursively calling interleave on the cdr's of both lists.
The second solution constructs the interleaved list one element at a time by swapping which list is passed in for lst1.
Thus, we can then grab elements from only lst1 to construct the list.
Scheme Lists & Quotation
As you read through this section, it may be difficult to understand the differences between the various representations of Scheme containers. We recommend that you use our online Scheme interpreter to see the box-and-pointer diagrams of pairs and lists that you're having a hard time visualizing! (Use the command
(autodraw)to toggle the automatic drawing of diagrams.)
Lists
Scheme lists are very similar to the linked lists we've been working with in
Python. Just like how a linked list is constructed of a series of Link
objects, a Scheme list is constructed with a series of pairs, which are created
with the constructor cons.
Scheme lists require that the cdr is either another list or nil, an empty list.
A list is displayed in the interpreter as a sequence of values (similar to the
__str__ representation of a Link object). For example,
scm> (cons 1 (cons 2 (cons 3 nil)))
(1 2 3)Here, we've ensured that the second argument of each cons expression is
another cons expression or nil.

We can retrieve values from our list with the car and cdr procedures, which
now work similarly to the Python Link's first and rest attributes.
(Curious about where these weird names come from? Check out their
etymology.)
scm> (define a (cons 1 (cons 2 (cons 3 nil)))) ; Assign the list to the name a
a
scm> a
(1 2 3)
scm> (car a)
1
scm> (cdr a)
(2 3)
scm> (car (cdr (cdr a)))
3If you do not pass in a pair or nil as the second argument to cons, it will
error:
scm> (cons 1 2)
Errorlist Procedure
There are a few other ways to create lists. The list procedure takes in an
arbitrary number of arguments and constructs a list with the values of these
arguments:
scm> (list 1 2 3)
(1 2 3)
scm> (list 1 (list 2 3) 4)
(1 (2 3) 4)
scm> (list (cons 1 (cons 2 nil)) 3 4)
((1 2) 3 4)Note that all of the operands in this expression are evaluated before being put into the resulting list.
Quote Form
We can also use the quote form to create a list, which will construct the exact
list that is given. Unlike with the list procedure, the argument to ' is
not evaluated.
scm> '(1 2 3)
(1 2 3)
scm> '(cons 1 2) ; Argument to quote is not evaluated
(cons 1 2)
scm> '(1 (2 3 4))
(1 (2 3 4))Built-In Procedures for Lists
There are a few other built-in procedures in Scheme that are used for lists. Try them out in the interpreter!
scm> (null? nil) ; Checks if a value is the empty list
True
scm> (append '(1 2 3) '(4 5 6)) ; Concatenates two lists
(1 2 3 4 5 6)
scm> (length '(1 2 3 4 5)) ; Returns the number of elements in a list
5Q3: Nested Lists
Create the nested list depicted below three different ways: using list, quote, and cons.
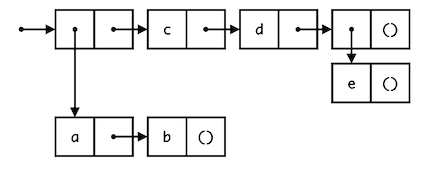
First, describe the list together: "It looks like there are four elements, and the first element is ..." If you get stuck, look at the hint below. (But try to describe it yourself first!)
a and
b, the second element is c, the third element is d, and the fourth element
is a list containing just e.
Next, use calls to list to construct this list. If you run this code and then (draw with-list) in
code.cs61a.org, the draw procedure will draw what you've built.
(define with-list
(list
(list 'a 'b) 'c 'd (list 'e)
)
)
; (draw with-list) ; Uncomment this line to draw with-lista and b: (list 'a 'b), a list containing e:
(list 'e), and the whole list of four elements: (list _ 'c 'd _). Try to
put these expressions together.
Now, use quote to construct this list.
(define with-quote
'(
(a b) c d (e)
)
)
; (draw with-quote) ; Uncomment this line to draw with-quote((a b) c d (e)). Quoting that expression will create the list.
Now, use cons to construct this list. Don't use list. You can use first in your answer.
(define first
(cons 'a (cons 'b nil))) (define with-cons
(cons
first (cons 'c (cons 'd (cons (cons 'e nil) nil)))
)
)
; (draw with-cons) ; Uncomment this line to draw with-consfirst is the first element of the result, so the answer takes the form:
first ____You can either fill in the blank with a quoted three-element list:
'(___ ___ ___)
c d (e)or with nested calls to cons:
(cons ___ (cons ___ (cons ___ nil)))
c d (e)Q4: Pair Up
Implement pair-up, which takes a list s. It returns a list of lists that
together contain all of the elements of s in order. Each list in the result
should have 2 elements. The last one can have up to 3.
Look at the examples together to make sure everyone understands what this procedure does.
Your Answer Run in 61A Code ;;; Return a list of pairs containing the elements of s.
;;;
;;; scm> (pair-up '(3 4 5 6 7 8))
;;; ((3 4) (5 6) (7 8))
;;; scm> (pair-up '(3 4 5 6 7 8 9))
;;; ((3 4) (5 6) (7 8 9))
(define (pair-up s)
(if (<= (length s) 3)
(list s)
(cons (list (car s) (car (cdr s))) (pair-up (cdr (cdr s))))
))
(expect (pair-up '(3 4 5 6 7 8)) ((3 4) (5 6) (7 8)) )
(expect (pair-up '(3 4 5 6 7 8 9)) ((3 4) (5 6) (7 8 9)) )pair-up takes a list (of numbers) and returns a list of lists, so when
(length s) is less than or equal to 3, return a list containing the list s.
For example, (pair-up (list 2 3 4)) should return ((2 3 4)).
Use (cons _ (pair-up _)) to create the result, where the first argument to
cons is a list with two elements: the (car s) and the (car (cdr s)). The
argument to pair-up is everything after the first two elements.
Discussion: What's the longest list s for which (pair-up (pair-up s))
will return a list with only one element? (Don't just guess and check; discuss!)
Q5: List Insert
Write a Scheme function that, when given an element, a list, and an index, inserts the element into the list at that index. You can assume that the index is in bounds for the list.
Your Answer Run in 61A Code (define (insert element lst index)
(if (= index 0)
(cons element lst)
(cons (car lst) (insert element (cdr lst) (- index 1))))
)
(expect (insert 2 '(1 7 9) 2) (1 7 2 9))
(expect (insert 'a '(b c) 0) (a b c))Submit Attendance
You're done! Excellent work this week. Please be sure to ask your section TA for the attendance form link and fill it out for credit. (one submission per person per section).