Discussion 9: Scheme, Scheme Lists

Reminder: We'll still use Pensieve, but we've removed the voice/video chat from Pensieve. Use Discord for voice chat with the course staff. It's more reliable and includes screensharing. Write to @discuss in the #discuss-queue channel on Discord at any time, and a member of the course staff will join your group's voice channel.

Pick someone in your group to join Discord. It's fine if multiple people join, but one is enough.

Now switch to Pensieve:

  • Everyone: Go to discuss.pensieve.co and log in with your @berkeley.edu email, then enter your group number. (Your group number is the number of your Discord channel.)

Once you're on Pensieve, you don't need to return to this page; Pensieve has all the same content (but more features). If for some reason Penseive doesn't work, return to this page and continue with the discussion.

Post in the #help channel on Discord if you have trouble.

Pro tip: Any of you can type a question into your group's Discord channel's text chat with the @discuss tag, and a member of the course staff will respond.

Getting Started

If you have only 1 or 2 people in your group, you can join the other group in the room with you.

Everybody say your name, and then figure out who most recently pet a dog. (Feel free to share dog photos. Even cat photos are acceptable.)

Scheme

Q1: Perfect Fit

Definition: A perfect square is k*k for some integer k.

Implement fit, which takes non-negative integers total and n. It returns whether there are n different positive perfect squares that sum to total.

Important: Don't use the Scheme interpreter to tell you whether you've implemented it correctly. Discuss! On the final exam, you won't have an interpreter.

Your Answer
Run in 61A Code
Solution 
;;; Return whether there are n perfect squares with no repeats that sum to total
(define (fit total n)
    (define (f total n k)
        (if (and (= n 0) (= total 0))
            #t
        (if (< total (* k k))
            #f
        (or (f total n (+ k 1)) (f (- total (* k k)) (- n 1) (+ k 1)))
        )))
    (f total n 1))

(expect (fit 10 2) #t)  ; 1*1 + 3*3
(expect (fit 9 1)  #t)  ; 3*3
(expect (fit 9 2)  #f)  ;
(expect (fit 9 3)  #f)  ; 1*1 + 2*2 + 2*2 doesn't count because of repeated 2*2
(expect (fit 25 1)  #t) ; 5*5
(expect (fit 25 2)  #t) ; 3*3 + 4*4

Use the (or _ _) special form to combine two recursive calls: one that uses k*k in the sum and one that does not. The first should subtract k*k from total and subtract 1 from n; the other should leaves total and n unchanged. In either case, add 1 to k.

Presentation Time: As a group, come up with one sentence describing how your implementation makes sure that all n positive perfect squares are different (no repeats). Once your group agrees on an answer (or wants help), send a message to the #discuss-queue channel with the @discuss tag, your discussion group number, and the message "It fits!" and a member of the course staff will join your voice channel to hear your explanation and give feedback.

Scheme Lists & Quotation

Scheme lists are linked lists. Lightning review:

  • nil and () are the same thing: the empty list.
  • (cons first rest) constructs a linked list with first as its first element. and rest as the rest of the list, which should always be a list.
  • (car s) returns the first element of the list s.
  • (cdr s) returns the rest of the list s.
  • (list ...) takes n arguments and returns a list of length n with those arguments as elements.
  • (append ...) takes n lists as arguments and returns a list of all of the elements of those lists.
  • (draw s) draws the linked list structure of a list s. It only works on code.cs61a.org/scheme. Try it now with something like (draw (cons 1 nil)).

Quoting an expression leaves it unevaluated. Examples:

  • 'four and (quote four) both evaluate to the symbol four.
  • '(2 3 4) and (quote (2 3 4)) both evaluate to a list containing three elements: 2, 3, and 4.
  • '(2 3 four) and (quote (2 3 four)) evaluate to a list containing 2, 3, and the symbol four.

Here's an important difference between list and quotation:

scm> (list 2 (+ 3 4))
(2 7)
scm> `(2 (+ 3 4))
(2 (+ 3 4))

Q2: Nested Lists

Create the nested list depicted below three different ways: using list, quote, and cons.


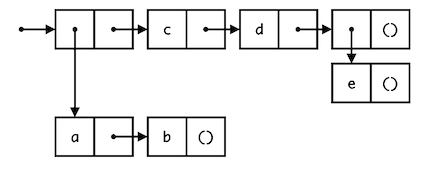
linked list

First, describe the list together: "It looks like there are four elements, and the first element is ..." If you get stuck, look at the hint below. (But try to describe it yourself first!)

A four-element list in which the first element is a list containing both a and b, the second element is c, the third element is d, and the fourth element is a list containing just e.

Next, use calls to list to construct this list. If you run this code and then (draw with-list) in code.cs61a.org, the draw procedure will draw what you've built.

Your Answer
Run in 61A Code
Solution 
(define with-list
    (list
        (list 'a 'b) 'c 'd (list 'e)
    )
)
; (draw with-list)  ; Uncomment this line to draw with-list
Every call to list creates a list, and there are three different lists in this diagram: a list containing a and b: (list 'a 'b), a list containing e: (list 'e), and the whole list of four elements: (list _ 'c 'd _). Try to put these expressions together.

Now, use quote to construct this list.

Your Answer
Run in 61A Code
Solution 
(define with-quote
    '(
        (a b) c d (e)
    )

)
; (draw with-quote)  ; Uncomment this line to draw with-quote
One quoted expression is enough, but it needs to match the structure of the linked list using Scheme notation. So, your task is to figure out how this list would be displayed in Scheme.
The nested list drawn above is a four-element list with lists as its first and last elements: ((a b) c d (e)). Quoting that expression will create the list.

Now, use cons to construct this list. Don't use list. You can use first in your answer.

Your Answer
Run in 61A Code
Solution 
(define first
   (cons 'a (cons 'b nil)))

(define with-cons
    (cons
        first (cons 'c (cons 'd (cons (cons 'e nil) nil)))
    )
)
; (draw with-cons)  ; Uncomment this line to draw with-cons
The provided first is the first element of the result, so the answer takes the form:

first ____

You can either fill in the blank with a quoted three-element list:

'(___ ___ ___) c d (e)

or with nested calls to cons:

(cons ___ (cons ___ (cons ___ nil))) c d (e)

Q3: Pair Up

Implement pair-up, which takes a list s. It returns a list of lists that together contain all of the elements of s in order. Each list in the result should have 2 elements. The last one can have up to 3.

Look at the examples together to make sure everyone understands what this procedure does.

Your Answer
Run in 61A Code
Solution 
;;; Return a list of pairs containing the elements of s.
;;;
;;; scm> (pair-up '(3 4 5 6 7 8))
;;; ((3 4) (5 6) (7 8))
;;; scm> (pair-up '(3 4 5 6 7 8 9))
;;; ((3 4) (5 6) (7 8 9))
(define (pair-up s)
    (if (<= (length s) 3)
        (list s)
        (cons (list (car s) (car (cdr s))) (pair-up (cdr (cdr s))))
    ))

(expect (pair-up '(3 4 5 6 7 8)) ((3 4) (5 6) (7 8)) )
(expect (pair-up '(3 4 5 6 7 8 9)) ((3 4) (5 6) (7 8 9)) )

pair-up takes a list (of numbers) and returns a list of lists, so when (length s) is less than or equal to 3, return a list containing the list s. For example, (pair-up (list 2 3 4)) should return ((2 3 4)).

Use (cons _ (pair-up _)) to create the result, where the first argument to cons is a list with two elements: the (car s) and the (car (cdr s)). The argument to pair-up is everything after the first two elements.

Discussion: What's the longest list s for which (pair-up (pair-up s)) will return a list with only one element? (Don't just guess and check; discuss!) Post your answer in your group's text chat.

Document the Occasion

Please all fill out the attendance form (one submission per person per week).

Important: Please help put the furniture in the room back where you found it before you leave. Thanks!