SQL Basics

Creating Tables

You can create SQL tables either from scratch or from existing tables.

The following statement creates a table by specifying column names and values without referencing another table. Each SELECT clause specifies the values for one row, and UNION is used to join rows together. The AS clauses give a name to each column; it need not be repeated in subsequent rows after the first.

CREATE TABLE [table_name] AS
  SELECT [val1] AS [column1], [val2] AS [column2], ... UNION
  SELECT [val3]             , [val4]             , ... UNION
  SELECT [val5]             , [val6]             , ...;

Let's say we want to make the following table called big_game which records the scores for the Big Game each year. This table has three columns: berkeley, stanford, and year.

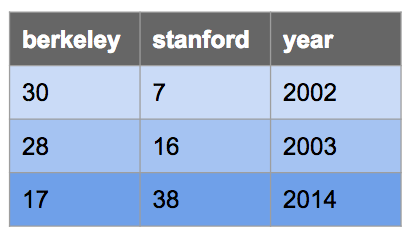
We could do so with the following CREATE TABLE statement:

CREATE TABLE big_game AS
  SELECT 30 AS berkeley, 7 AS stanford, 2002 AS year UNION
  SELECT 28,             16,            2003         UNION
  SELECT 17,             38,            2014;

Selecting From Tables

More commonly, we will create new tables by selecting specific columns that we want from existing tables by using a SELECT statement as follows:

SELECT [columns] FROM [tables] WHERE [condition] ORDER BY [columns] LIMIT [limit];

Let's break down this statement:

• SELECT [columns] tells SQL that we want to include the given columns in our output table; [columns] is a comma-separated list of column names, and * can be used to select all columns
• FROM [table] tells SQL that the columns we want to select are from the given table; see the joins section to see how to select from multiple tables
• WHERE [condition] filters the output table by only including rows whose values satisfy the given [condition], a boolean expression
• ORDER BY [columns] orders the rows in the output table by the given comma-separated list of columns
• LIMIT [limit] limits the number of rows in the output table by the integer [limit]

Here are some examples:

Select all of Berkeley's scores from the big_game table, but only include scores from years past 2002:

sqlite> SELECT berkeley FROM big_game WHERE year > 2002;
28
17

Select the scores for both schools in years that Berkeley won:

sqlite> SELECT berkeley, stanford FROM big_game WHERE berkeley > stanford;
30|7
28|16

Select the years that Stanford scored more than 15 points:

sqlite> SELECT year FROM big_game WHERE stanford > 15;
2003
2014

SQL operators

Expressions in the SELECT, WHERE, and ORDER BY clauses can contain one or more of the following operators:

• comparison operators: =, >, <, <=, >=, <> or != ("not equal")
• boolean operators: AND, OR
• arithmetic operators: +, -, *, /
• concatenation operator: ||

Here are some examples:

Output the ratio of Berkeley's score to Stanford's score each year:

sqlite> select berkeley * 1.0 / stanford from big_game;
0.447368421052632
1.75
4.28571428571429

Output the sum of scores in years where both teams scored over 10 points:

sqlite> select berkeley + stanford from big_game where berkeley > 10 and stanford > 10;
55
44

Output a table with a single column and single row containing the value "hello world":

sqlite> SELECT "hello" || " " || "world";
hello world

Joins

To select data from multiple tables, we can use joins. There are many types of joins, but the only one we'll worry about is the inner join. To perform an inner join on two on more tables, simply list them all out in the FROM clause of a SELECT statement:

SELECT [columns] FROM [table1], [table2], ... WHERE [condition] ORDER BY [columns] LIMIT [limit];

We can select from multiple different tables or from the same table multiple times.

Let's say we have the following table that contains the names of head football coaches at Cal since 2002:

CREATE TABLE coaches AS
  SELECT "Jeff Tedford" AS name, 2002 as start, 2012 as end UNION
  SELECT "Sonny Dykes"         , 2013         , 2016        UNION
  SELECT "Justin Wilcox"       , 2017         , null;

When we join two or more tables, the default output is a cartesian product. For example, if we joined big_game with coaches, we'd get the following:

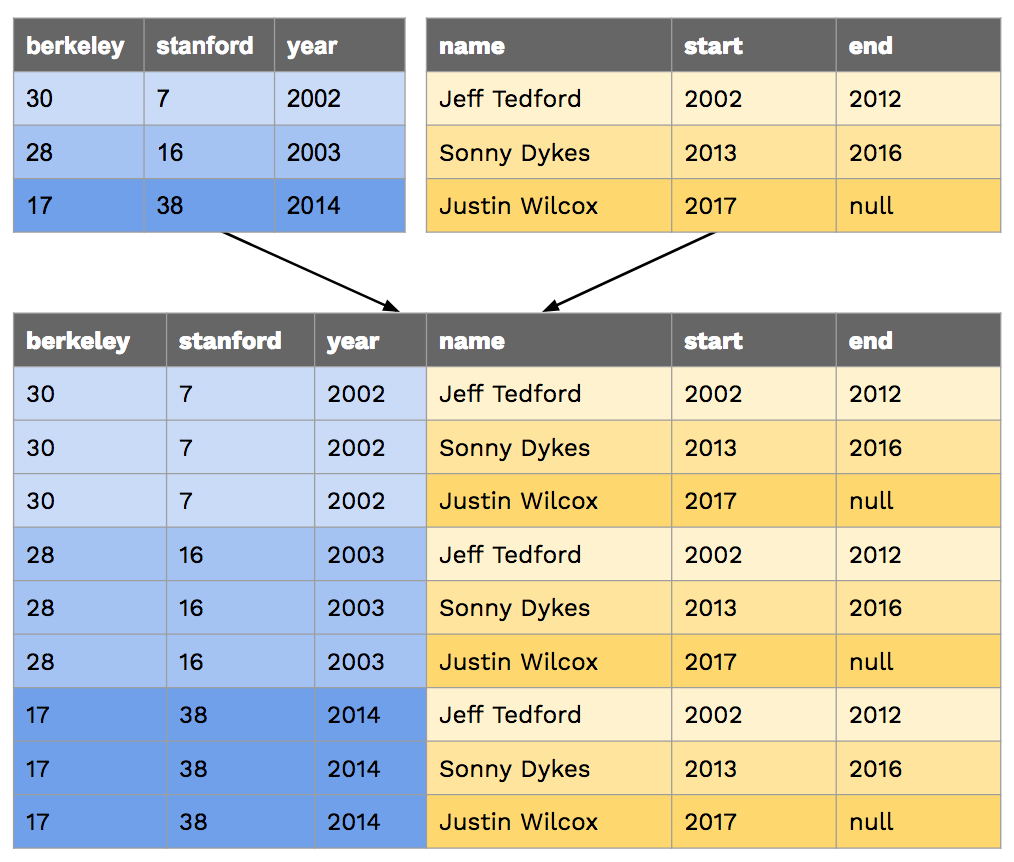
If we want to match up each game with the coach that season, we'd have to compare columns from the two tables in the WHERE clause:

sqlite> SELECT * FROM big_game, coaches WHERE year >= start AND year <= end;
17|38|2014|Sonny Dykes|2013|2016
28|16|2003|Jeff Tedford|2002|2012
30|7|2002|Jeff Tedford|2002|2012

The following query outputs the coach and year for each Big Game win recorded in big_game:

sqlite> SELECT name, year FROM big_game, coaches
...>        WHERE berkeley > stanford AND year >= start AND year <= end;
Jeff Tedford|2003
Jeff Tedford|2002

In the queries above, none of the column names are ambiguous. For example, it is clear that the name column comes from the coaches table because there isn't a column in the big_game table with that name. However, if a column name exists in more than one of the tables being joined, or if we join a table with itself, we must disambiguate the column names using aliases.

For examples, let's find out what the score difference is for each team between a game in big_game and any previous games. Since each row in this table represents one game, in order to compare two games we must join big_game with itself:

sqlite> SELECT b.Berkeley - a.Berkeley, b.Stanford - a.Stanford, a.Year, b.Year
...>        FROM big_game AS a, big_game AS b WHERE a.Year < b.Year;
-11|22|2003|2014
-13|21|2002|2014
-2|9|2002|2003

In the query above, we give the alias a to the first big_game table and the alias b to the second big_game table. We can then reference columns from each table using dot notation with the aliases, e.g. a.Berkeley, a.Stanford, and a.Year to select from the first table.

SQL Aggregation

Previously, we have been dealing with queries that process one row at a time. When we join, we make pairwise combinations of all of the rows. When we use WHERE, we filter out certain rows based on the condition. Alternatively, applying an aggregate function such as MAX(column) combines the values in multiple rows.

By default, we combine the values of the entire table. For example, if we wanted to count the number of flights from our flights table, we could use:

sqlite> SELECT COUNT(*) from FLIGHTS;
13

What if we wanted to group together the values in similar rows and perform the aggregation operations within those groups? We use a GROUP BY clause.

Here's another example. For each unique departure, collect all the rows having the same departure airport into a group. Then, select the price column and apply the MIN aggregation to recover the price of the cheapest departure from that group. The end result is a table of departure airports and the cheapest departing flight.

sqlite> SELECT departure, MIN(price) FROM flights GROUP BY departure;
AUH|932
LAS|50
LAX|89
SEA|32
SFO|40
SLC|42

Just like how we can filter out rows with WHERE, we can also filter out groups with HAVING. Typically, a HAVING clause should use an aggregation function. Suppose we want to see all airports with at least two departures:

sqlite> SELECT departure FROM flights GROUP BY departure HAVING COUNT(*) >= 2;
LAX
SFO
SLC

Note that the COUNT(*) aggregate just counts the number of rows in each group. Say we want to count the number of distinct airports instead. Then, we could use the following query:

sqlite> SELECT COUNT(DISTINCT departure) FROM flights;
6

This enumerates all the different departure airports available in our flights table (in this case: SFO, LAX, AUH, SLC, SEA, and LAS).

Usage

First, check that a file named sqlite_shell.py exists alongside the assignment files. If you don't see it, or if you encounter problems with it, scroll down to the Troubleshooting section to see how to download an official precompiled SQLite binary before proceeding.

You can start an interactive SQLite session in your Terminal or Git Bash with the following command:

python3 sqlite_shell.py

While the interpreter is running, you can type .help to see some of the commands you can run.

To exit out of the SQLite interpreter, type .exit or .quit or press Ctrl-C. Remember that if you see ...> after pressing enter, you probably forgot a ;.

You can also run all the statements in a .sql file by doing the following: (Here we're using the lab13.sql file as an example.)

1. Runs your code and then exits SQLite immediately afterwards.

   python3 sqlite_shell.py < lab13.sql

2. Runs your code and then opens an interactive SQLite session, which is similar to running Python code with the interactive -i flag.

   python3 sqlite_shell.py --init lab13.sql

SELECT _____ FROM _____ WHERE _____ GROUP BY _____ HAVING _____;

1. Use FROM and WHERE to combine the information in the finals and sizes tables.
2. Use GROUP BY and HAVING to create one group for each course that has at least 1,000 seats.
3. Use SELECT to put the name of the course in the output.

SELECT course, _____ AS remaining
  FROM _____ WHERE _____ GROUP BY _____;

1. Use FROM and WHERE to combine the information in the finals and sizes tables.
2. Use GROUP BY to create one group for each course.
3. Use SELECT to compute the total number of seats in all final rooms for that course except the largest one.

SELECT course, COUNT(DISTINCT _____) AS shared
  FROM finals AS a, finals AS b
  WHERE _____ GROUP BY _____;

1. Use FROM and WHERE to create a row for each instance of two courses sharing a final room.
2. Use GROUP BY to create one group for each course.
3. Use SELECT to compute the total number of rooms for that course which are also used by another course

  SELECT _____ || " and " || _____ || " together have " || (_____) || " seats" AS rooms
    FROM sizes AS a, sizes AS b WHERE _____
    ORDER BY _____ DESC;

1. Use FROM and WHERE to create a row for each pair of different rooms (in alphabetical order) with at least 1,000 seats total.
2. No grouping is needed
3. Use SELECT to compute the total number of rooms for that course which are also used by another course