Study Guide: Functions and Control
Instructions
This is a study guide with links to past lectures, assignments, and handouts, as well as additional practice problems to assist you in learning the concepts.
Draw environment diagrams automatically with Python Tutor.
Assignments
Important: For solutions to these assignments once they have been released, see the main website
Handouts
Lectures
Readings
Guides
return vs. print
A lot of students were confused about the return statement (more specifically
return vs. print).
return statements allow the programmer to return a value from a function. You
can take the returned value and save it to a variable or do whatever you want
with it.
Think of it as a store. When you return something at the store, that item that you return will probably be purchased by someone else and they will use it however they want. (I know the analogy is not so great).
print statements on the other hand just print what you want to the screen and
returns None. It doesn't allow you to actually use the value that you printed
elsewhere. Once a value is printed, Python can no longer use it for
computation.
Two different functions will be used to illustrate the difference.
The first function example will return a string:
def some_function():
return 'I love John DeNero'Calling some_function returns the string, 'I love John DeNero', so I can also
bind that return value to a name.
my_love = some_function()Now, the variable my_love is set to the return value of some_function(), in
this case it is 'I love John DeNero'. So my_love = 'I love John DeNero'.
The second function example will print a string:
def some_function():
print('I love John DeNero')Calling some_function() now will print 'I love John DeNero' on the
terminal and then return None. (Recall that, if a function has no return
statement, it will return None.) This time, binding the return value to a
name has a different result.
my_love = some_function()It will print 'I love John DeNero' on the terminal and bind my_love = None.
It is important to note that return statements will terminate the function.
def some_function():
return 5
return 3It will return 5 and end the function without ever returning 3.
Boolean context
Boolean contexts are "places in Python code where you place an expression but all that matters about that expression is whether it's true or false."
Here's an example from lecture of a function containing an if statement with
two boolean contexts.
def absolute_value(x):
"""Return the absolute value of x."""
if x < 0:
return -x
elif x == 0:
return 0
else:
return xIn the if clause, Python asks, "Is x < 0 a true value or a false
value?" This depends on the value of x. Suppose we have x = 3.
>>> x = 3
>>> x < 0
FalsePython evaluates the call expression x < 0 to False. Now, we need to ask
the question, is False a false value? This might seem like an unusual
question to ask, but it's actually a very subtle step.
In Python, false values include the following values (more to come):
False, 0, '', NoneEverything else is a true value.
Because we know that False is a false value, the entire expression x < 0
is a false value in boolean context.
Let's look at another example to see why boolean context and true value/false value distinction matters. Suppose we want to evaluate the following boolean expression.
>>> print('hi') or 25The or operator contains two boolean contexts, one on each side of the or.
Let's evaluate this expression.
print('hi') prints the string 'hi' to the terminal and returns None.
Because None is a false value in Python, the first boolean context is false.
25 evaluates to the number 25. Because 25 is a non-zero number, it is a true
value in Python and so the second boolean context is true.
The final value that is returned from the entire or is 25 because Python uses
the boolean context only to determine how to interpret the value in the context
of an or expression. 25 is not the same as True; it just evaluates to a
true value in boolean context.
WWPD Questions
For each of the expressions below, write the output displayed by the interactive Python interpreter when the expression is evaluated. The output may have multiple lines. If an error occurs, write "Error", but include all output displayed before the error. If a function value is displayed, write "Function".
Recall: The interactive interpreter displays the value of a successfully
evaluated expression, unless it is None.
Assume that you have started python3 and executed the following statements:
Q1: Multiples
from math import sqrt
x = 15
def square(x):
return print(x * x)
def multiply(x):
x_new = x * 2
return x * 3>>> print(print(3, 5))
______3 5
None
>>> square(x)
______225
>>> True and 17
______17>>> print(multiply(x))
______45
>>> multiply(multiply(3))
______27
>>> print(square(multiply(2)), 8) + 3
______36
None 8
ErrorQ2: Quizzical
x = 2
def take_quiz(x):
print(x * 10)
if x * 10 >= 100:
return 'Good job!'
return 'Go to office hours!'
def office_hour(x):
while x < 10:
x = x + 3
return print(take_quiz(x))>>> pow(print(0, 0), 0)
______0 0
Error
>>> office_hour(4)
______100
Good job!>>> print(take_quiz(x))
______20
Go to office hours!
>>> print(office_hour(x))
______110
Good job!
None>>> office_hour(office_hour(x))
______110
Good job!
Error>>> take_quiz(-3) and print(office_hour(x))
______-30
110
Good Job!
NoneQ3: There can only be Wan
Hint: Draw environment diagrams to track progress! Don't just quietly recite the names to yourself, as names that sound similar can easily be mixed up!
def wan1(wan1, wan11):
return wan1 == wan11
def wan11(wan11, wan1):
return wan1 / wan11
one, wan, won = 1, 3, 17
def derek(wan, won, one):
print(wan1(wan, wan11(won, 1)))
return wan11(one, wan1)>>> print(one or wan11(0, one))
______1
>>> print(wan1(one, wan11(one, one)))
______True>>> print(print(wan - won), wan1)
______-14
None Function>>> derek(1, 1, 2)
______True
Error>>> derek(wan, 2, one)
______False
ErrorQ4: Whoos hat?
s = 2
def hat(s):
while s > 0:
whoos(s)
s = s - 1
return whoos(s)
def someones(their, hat):
his, her = their, hat
hat = print(his or her) and her or his
if hat:
return 'hat'
def whoos(hat):
return print(hat)>>> print(s) or 1 / 0
______2
Error
>>> 0 or 2 == True and print(5)
______False>>> her, cat = 'her', print('theirs') or 'his'
______theirs
>>> someones(her, cat)
______her
'hat'>>> hat(s)
______2
1
0>>> print(whoos(hat), someones(cat, hat))
______Function
his
None hatQ5: Out at the Ballgame
def announce(score, inning):
hits = score * 3 % inning - 1
print('The Giants have ' + str(score) + ' runs!')
if hits < 2:
jumbotron_text = print('That\'s the end of the inning!')
inning = inning + 1
return jumbotron_text
else:
score = score + hits % 3
crowd_noise = print('The Giants now have: ' + str(score))
print(str(crowd_noise))
return score
def player(hits, inning):
if hits < 2:
print('I need to practice in the batting cage!')
score = hits * 2 + 1
saying = announce(score, inning)
return saying * 2>>> print(3, print(5 % 3))
______2
3 None>>> player(0, 0)
______I need to practice in the batting cage!
Error>>> player(3, 2)
______The Giants have 7 runs!
That's the end of the inning!
Error>>> player(5, 9) - 5
______The Giants have 11 runs!
The Giants now have 13
None
21>>> player(announce(15, 8), 4)
______The Giants have 15 runs!
The Giants have 16
None
The Giants have 33 runs!
The Giants now have 35
None
70Practice Problems
Easy
Q6: Distance
Implement a function called distance(x1, y1, x2, y2):
x1andy1form an x-y coordinate pairx2andy2form an x-y coordinate pair
distance returns the Euclidean distance between the two points. Use the
following formula:
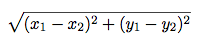
from math import sqrt
def distance(x1, y1, x2, y2):
"""Calculates the Euclidian distance between two points (x1, y1) and (x2, y2)
>>> distance(1, 1, 1, 2)
1.0
>>> distance(1, 3, 1, 1)
2.0
>>> distance(1, 2, 3, 4)
2.8284271247461903
"""
"*** YOUR CODE HERE ***"
return sqrt(square(x1-x2) + square(y1-y2))Q7: Distance (3D)
Now, let us edit this program to get the distance between two
3-dimensional coordinates. Your distance3d function should take six
arguments and compute the following:
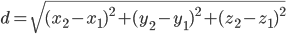
def distance3d(x1, y1, z1, x2, y2, z2):
"""Calculates the 3D Euclidian distance between two points (x1, y1, z1) and
(x2, y2, z2).
>>> distance3d(1, 1, 1, 1, 2, 1)
1.0
>>> distance3d(2, 3, 5, 5, 8, 3)
6.164414002968976
"""
"*** YOUR CODE HERE ***"
return sqrt(square(x1-x2) + square(y1-y2) + square(z1-z2))Q8: Harmony
Implement harmonic, which returns the harmonic mean of two positive numbers
x and y. The harmonic mean of 2 numbers is 2 divided by the sum of the
reciprocals of the numbers. (The reciprocal of x is 1/x.)
def harmonic(x, y):
"""Return the harmonic mean of x and y.
>>> harmonic(2, 6)
3.0
>>> harmonic(1, 1)
1.0
>>> harmonic(2.5, 7.5)
3.75
>>> harmonic(4, 12)
6.0
"""
"*** YOUR CODE HERE ***"
return 2/(1/x + 1/y)Q9: Environments
Python Tutor is a great visualization tool for environment diagrams. Paste in your Python code and it will generate an environment diagram you can walk through step-by-step! Use it to help you check your answers!
Try drawing environment diagrams for the following examples and predicting what Python will output:
>>> def square(x):
... return x * x
>>> def double(x):
... return x + x
>>> a = square(double(4))
>>> a
______64>>> x, y = 4, 3
>>> def reassign(arg1, arg2):
... x = arg1
... y = arg2
>>> reassign(5, 6)
>>> x
______4
>>> y
______3>>> def f(x):
... f(x)
>>> print, f = f, print
>>> a = f(4)
______4
>>> a
______# Nothing shows up, because a = None
>>> b = print(4)
______4
>>> b
______# Nothing shows up, because b = NoneQ10: Fix the Bug
The following snippet of code doesn't work! Figure out what is wrong and fix the bugs.
def compare(a, b):
""" Compares if a and b are equal.
>>> compare(4, 2)
'not equal'
>>> compare(4, 4)
'equal'
"""
if a = b:
return 'equal'
return 'not equal'The line a = b will cause a SyntaxError. Instead, it should be
if a == b:Q11: Last square
Implement the function last_square, which takes as input a positive
integer and returns the largest perfect square less than its argument.
A perfect square is any integer multiplied by itself:
Hint: If you're stuck, try writing a function that prints out the
first 5 perfect squares using a while statement: 1, 4, 9, 16, 25.
Then, adapt that while statement to this question by changing the
header.
def last_square(x):
"""Return the largest perfect square less than X, where X>0.
>>> last_square(10)
9
>>> last_square(39)
36
>>> last_square(100)
81
>>> result = last_square(2) # Return, don't print
>>> result
1
>>> cases = [(1, 0), (2, 1), (3, 1), (4, 1), (5, 4), (6, 4),
... (10, 9), (17, 16), (26, 25), (36, 25), (46, 36)]
>>> [last_square(s) == t for s, t in cases].count(False)
0
"""
"*** YOUR CODE HERE ***"
k = 0
while k * k < x:
k = k + 1
return (k-1) * (k-1)We iterate over perfect squares until we find the first one larger or equal to the input. The answer is then the square before that one. This solution is inefficient, but an efficient solution requires taking a square root.
Q12: Overlaps
An open interval is a range of numbers that does not include its end points.
For example, (10, 15) stands for all numbers that are strictly greater than 10
and strictly less than 15. Two intervals overlap if they contain any points
in common. For example (10, 15) overlaps (14, 16), but not (1, 5) or (15, 16).
The intervals (10, 10) or (10, 9) contain no numbers, since nothing is both
greater than and less than 10, or greater than 10 and less than 9. Implement
the function overlaps to take four numbers as arguments, representing the
bounds of two intervals, and return True if the intervals overlap and False
otherwise.
def overlaps(low0, high0, low1, high1):
"""Return whether the open intervals (LOW0, HIGH0) and (LOW1, HIGH1)
overlap.
>>> overlaps(10, 15, 14, 16)
True
>>> overlaps(10, 15, 1, 5)
False
>>> overlaps(10, 10, 9, 11)
False
>>> result = overlaps(1, 5, 0, 3) # Return, don't print
>>> result
True
>>> [overlaps(a0, b0, a1, b1) for a0, b0, a1, b1 in
... ( (1, 4, 2, 3), (1, 4, 0, 2), (1, 4, 3, 5), (0.1, 0.4, 0.2, 0.3),
... (2, 3, 1, 4), (0, 2, 1, 4), (3, 5, 1, 4) )].count(False)
0
>>> [overlaps(a0, b0, a1, b1) for a0, b0, a1, b1 in
... ( (1, 4, -1, 0), (1, 4, 5, 6), (1, 4, 4, 5), (1, 4, 0, 1),
... (-1, 0, 1, 4), (5, 6, 1, 4), (4, 5, 1, 4), (0, 1, 1, 4),
... (5, 5, 3, 6), (5, 3, 4, 6), (5, 5, 5, 5),
... (3, 6, 5, 5), (4, 6, 5, 3), (0.3, 0.6, 0.5, 0.5) )].count(True)
0
"""
"*** YOUR CODE HERE ***"
return low1 < min(high0, high1) > low0There are many solutions to this problem. One way to look at it is to consider
conditions under which the intervals don't overlap. Clearly for two non-empty
not to overlap, one has to come entirely before the other. This becomes high1
<= low0 or high0 <= low1, which when negated is high1 > low0 and high1 >
low1. In addition, both lower bounds must be less than their respective upper
bounds (or the intervals are empty). The solution given combines these
observations.
Q13: Triangular numbers
The nth triangular number is defined as the sum of all integers from 1 to n, i.e.
1 + 2 + ... + nThe closed-form formula for the nth triangular number is
(n + 1) * n / 2Define triangular_sum, which takes an integer n and returns the sum of the
first n triangular numbers, while printing each of the triangular numbers
between 1 and the nth triangular number.
def triangular_sum(n):
"""
>>> t_sum = triangular_sum(5)
1
3
6
10
15
>>> t_sum
35
"""
"*** YOUR CODE HERE ***"
count = 1
t_sum = 0
while count <= n:
t_number = count * (count + 1) // 2
print(t_number)
t_sum += t_number
count += 1
return t_sumMedium
Q14: Same hailstone
Implement same_hailstone, which returns whether positive integer arguments
a and b are part of the same hailstone sequence. A hailstone sequence is
defined in Homework 1 as the following:
- Pick a positive integer
nas the start. - If
nis even, divide it by 2. - If
nis odd, multiply it by 3 and add 1. - Continue this process until
nis 1.
def same_hailstone(a, b):
"""Return whether a and b are both members of the same hailstone
sequence.
>>> same_hailstone(10, 16) # 10, 5, 16, 8, 4, 2, 1
True
>>> same_hailstone(16, 10) # order doesn't matter
True
>>> result = same_hailstone(3, 19) # return, don't print
>>> result
False
Extra tests:
>>> same_hailstone(19, 3)
False
>>> same_hailstone(4858, 61)
True
>>> same_hailstone(7, 6)
False
"""
"*** YOUR CODE HERE ***"
return in_hailstone(a, b) or in_hailstone(b, a)
def in_hailstone(a, b):
"""Return whether b is in hailstone sequence of a."""
while a > 1:
if a == b:
return True
elif a % 2 == 0:
a = a // 2
else:
a = a * 3 + 1
return FalseQ15: Pi Fraction
Complete the implementation of pi_fraction, which takes a positive number
gap and prints the fraction that is no more than gap away from pi and has
the smallest possible positive integer denominator. See the doctests for the
format of the printed output.
Hint: If you want to find the nearest integer to a number, use the built-in
round function. It's possible to solve this problem without using round.
You may change the starter implementation if you wish.
from math import pi
def pi_fraction(gap):
"""Print the fraction within gap of pi that has the smallest denominator.
>>> pi_fraction(0.01)
22 / 7 = 3.142857142857143
>>> pi_fraction(1)
3 / 1 = 3.0
>>> pi_fraction(1/8)
13 / 4 = 3.25
>>> pi_fraction(1e-6)
355 / 113 = 3.1415929203539825
>>> pi_fraction(1e-3)
201 / 64 = 3.140625
>>> pi_fraction(1/32)
19 / 6 = 3.1666666666666665
"""
numerator, denominator = 3, 1
"*** YOUR CODE HERE ***"
while abs(numerator/denominator-pi) > gap:
denominator = denominator + 1
numerator = round(pi * denominator) print(numerator, '/', denominator, '=', numerator/denominator)This implementation repeatedly increases denominator until the nearest
fraction to pi is within gap.