Discussion 7: Mutable Trees, Linked Lists

Trees (Class)

A Tree instance has two instance attributes:
  • label is the value stored at the root of the tree.
  • branches is a list of Tree instances that hold the labels in the rest of the tree.

The Tree class (with its __repr__ and __str__ methods omitted) is defined as:

class Tree:
    """A tree has a label and a list of branches.

    >>> t = Tree(3, [Tree(2, [Tree(5)]), Tree(4)])
    >>> t.label
    3
    >>> t.branches[0].label
    2
    >>> t.branches[1].is_leaf()
    True
    """
    def __init__(self, label, branches=[]):
        self.label = label
        for branch in branches:
            assert isinstance(branch, Tree)
        self.branches = list(branches)

    def is_leaf(self):
        return not self.branches

To construct a Tree instance from a label x (any value) and a list of branches bs (a list of Tree instances) and give it the name t, write t = Tree(x, bs).

For a tree t:

  • Its root label can be any value, and t.label evaluates to it.
  • Its branches are always Tree instances, and t.branches evaluates to the list of its branches.
  • t.is_leaf() returns True if t.branches is empty and False otherwise.
  • To construct a leaf with label x, write Tree(x).

Displaying a tree t:

  • repr(t) returns a Python expression that evaluates to an equivalent tree.
  • str(t) returns one line for each label indented once more than its parent with children below their parents.
>>> t = Tree(3, [Tree(1, [Tree(4), Tree(1)]), Tree(5, [Tree(9)])])

>>> t         # displays the contents of repr(t)
Tree(3, [Tree(1, [Tree(4), Tree(1)]), Tree(5, [Tree(9)])])

>>> print(t)  # displays the contents of str(t)
3
  1
    4
    1
  5
    9

Changing (also known as mutating) a tree t:

  • t.label = y changes the root label of t to y (any value).
  • t.branches = ns changes the branches of t to ns (a list of Tree instances).
  • Mutation of t.branches will change t. For example, t.branches.append(Tree(y)) will add a leaf labeled y as the right-most branch.
  • Mutation of any branch in t will change t. For example, t.branches[0].label = y will change the root label of the left-most branch to y.
>>> t.label = 3.0
>>> t.branches[1].label = 5.0
>>> t.branches.append(Tree(2, [Tree(6)]))
>>> print(t)
3.0
  1
    4
    1
  5.0
    9
  2
    6

Here is a summary of the differences between the tree data abstraction implemented as a functional abstraction vs. implemented as a class:

- Tree constructor and selector functions Tree class
Constructing a tree To construct a tree given a label and a list of branches, we call tree(label, branches) To construct a tree object given a label and a list of branches, we call Tree(label, branches) (which calls the Tree.__init__ method).
Label and branches To get the label or branches of a tree t, we call label(t) or branches(t) respectively To get the label or branches of a tree t, we access the instance attributes t.label or t.branches respectively.
Mutability The functional tree data abstraction is immutable (without violating its abstraction barrier) because we cannot assign values to call expressions The label and branches attributes of a Tree instance can be reassigned, mutating the tree.
Checking if a tree is a leaf To check whether a tree t is a leaf, we call the function is_leaf(t) To check whether a tree t is a leaf, we call the method t.is_leaf(). This method can only be called on Tree objects.

Q1: Is BST

Write a function is_bst, which takes a Tree t and returns True if, and only if, t is a valid binary search tree, which means that:

  • Each node has at most two children (a leaf is automatically a valid binary search tree)
  • The children are valid binary search trees
  • For every node, the entries in that node's left child are less than or equal to the label of the node
  • For every node, the entries in that node's right child are greater than the label of the node

An example of a BST is:

bst

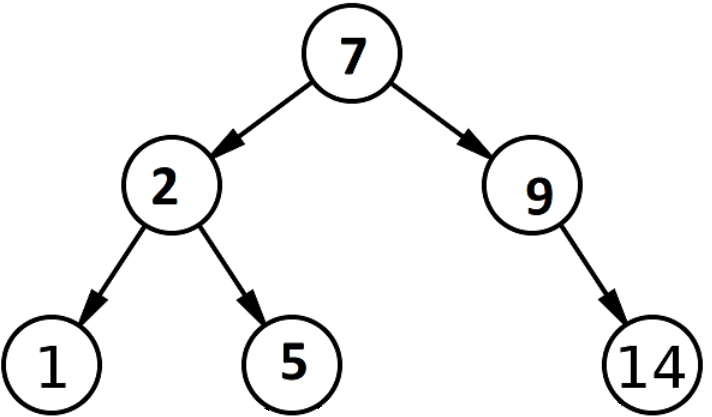
Note that, if a node has only one child, that child could be considered either the left or right child. You should take this into consideration.

Hint: It may be helpful to write helper functions bst_min and bst_max that return the minimum and maximum, respectively, of a Tree if it is a valid binary search tree.

Your Answer
Run in 61A Code
Solution 
def is_bst(t):
    """Returns True if the Tree t has the structure of a valid BST.

    >>> t1 = Tree(6, [Tree(2, [Tree(1), Tree(4)]), Tree(7, [Tree(7), Tree(8)])])
    >>> is_bst(t1)
    True
    >>> t2 = Tree(8, [Tree(2, [Tree(9), Tree(1)]), Tree(3, [Tree(6)]), Tree(5)])
    >>> is_bst(t2)
    False
    >>> t3 = Tree(6, [Tree(2, [Tree(4), Tree(1)]), Tree(7, [Tree(7), Tree(8)])])
    >>> is_bst(t3)
    False
    >>> t4 = Tree(1, [Tree(2, [Tree(3, [Tree(4)])])])
    >>> is_bst(t4)
    True
    >>> t5 = Tree(1, [Tree(0, [Tree(-1, [Tree(-2)])])])
    >>> is_bst(t5)
    True
    >>> t6 = Tree(1, [Tree(4, [Tree(2, [Tree(3)])])])
    >>> is_bst(t6)
    True
    >>> t7 = Tree(2, [Tree(1, [Tree(5)]), Tree(4)])
    >>> is_bst(t7)
    False
    """
    def bst_min(t):
        """Returns the min of t, if t has the structure of a valid BST."""
        if t.is_leaf():
            return t.label
        return min(t.label, bst_min(t.branches[0]))

    def bst_max(t):
        """Returns the max of t, if t has the structure of a valid BST."""
        if t.is_leaf():
            return t.label
        return max(t.label, bst_max(t.branches[-1]))

    if t.is_leaf():
        return True
    if len(t.branches) == 1:
        c = t.branches[0]
        return is_bst(c) and (bst_max(c) <= t.label or bst_min(c) > t.label)
    elif len(t.branches) == 2:
        c1, c2 = t.branches
        valid_branches = is_bst(c1) and is_bst(c2)
        return valid_branches and bst_max(c1) <= t.label and bst_min(c2) > t.label
    else:
        return False

Q2: Prune Small

Complete the function prune_small that takes in a Tree t and a number n and prunes t mutatively. If t or any of its branches has more than n branches, the n branches with the smallest labels should be kept and any other branches should be pruned, or removed, from the tree.

Your Answer
Run in 61A Code
Solution 
def prune_small(t, n):
    """Prune the tree mutatively, keeping only the n branches
    of each node with the smallest labels.

    >>> t1 = Tree(6)
    >>> prune_small(t1, 2)
    >>> t1
    Tree(6)
    >>> t2 = Tree(6, [Tree(3), Tree(4)])
    >>> prune_small(t2, 1)
    >>> t2
    Tree(6, [Tree(3)])
    >>> t3 = Tree(6, [Tree(1), Tree(3, [Tree(1), Tree(2), Tree(3)]), Tree(5, [Tree(3), Tree(4)])])
    >>> prune_small(t3, 2)
    >>> t3
    Tree(6, [Tree(1), Tree(3, [Tree(1), Tree(2)])])
    """
    while len(t.branches) > n:
        largest = max(t.branches, key=lambda x: x.label)
        t.branches.remove(largest)
    for b in t.branches:
        prune_small(b, n)

Linked Lists

A linked list is a Link object or Link.empty.

You can mutate a Link object s in two ways:

  • Change the first element with s.first = ...
  • Change the rest of the elements with s.rest = ...

You can make a new Link object by calling Link:

  • Link(4) makes a linked list of length 1 containing 4.
  • Link(4, s) makes a linked list that starts with 4 followed by the elements of linked list s.

Here is the implementation of the Link class:

class Link:
    """A linked list is either a Link object or Link.empty

    >>> s = Link(3, Link(4, Link(5)))
    >>> s.rest
    Link(4, Link(5))
    >>> s.rest.rest.rest is Link.empty
    True
    >>> s.rest.first * 2
    8
    >>> print(s)
    <3 4 5>
    """
    empty = ()

    def __init__(self, first, rest=empty):
        assert rest is Link.empty or isinstance(rest, Link)
        self.first = first
        self.rest = rest

    def __repr__(self):
        if self.rest:
            rest_repr = ', ' + repr(self.rest)
        else:
            rest_repr = ''
        return 'Link(' + repr(self.first) + rest_repr + ')'

    def __str__(self):
        string = '<'
        while self.rest is not Link.empty:
            string += str(self.first) + ' '
            self = self.rest
        return string + str(self.first) + '>'

Q3: Sum Two Ways

Implement both sum_rec and sum_iter. Each one takes a linked list of numbers s and a non-negative integer k and returns the sum of the first k elements of s. If there are fewer than k elements in s, all of them are summed. If k is 0 or s is empty, the sum is 0.

Use recursion to implement sum_rec. Don't use recursion to implement sum_iter; use a while loop instead.

Your Answer
Run in 61A Code
Solution 
def sum_rec(s, k):
    """Return the sum of the first k elements in s.

    >>> a = Link(1, Link(6, Link(8)))
    >>> sum_rec(a, 2)
    7
    >>> sum_rec(a, 5)
    15
    >>> sum_rec(Link.empty, 1)
    0
    """
    # Use a recursive call to sum_rec; don't call sum_iter
    if k == 0 or s is Link.empty:
        return 0
    return s.first + sum_rec(s.rest, k - 1)

def sum_iter(s, k):
    """Return the sum of the first k elements in s.

    >>> a = Link(1, Link(6, Link(8)))
    >>> sum_iter(a, 2)
    7
    >>> sum_iter(a, 5)
    15
    >>> sum_iter(Link.empty, 1)
    0
    """
    # Don't call sum_rec or sum_iter
    total = 0
    while k > 0 and s is not Link.empty:
        total, s, k = total + s.first, s.rest, k - 1
    return total

Q4: Overlap

Implement overlap, which takes two linked lists of numbers called s and t that are sorted in increasing order and have no repeated elements within each list. It returns the count of how many numbers appear in both lists.

This can be done in linear time in the combined length of s and t.

You can use either recursion or iteration. If you finish early, implement it the other way! Your Answer
Run in 61A Code
Solution 
def overlap(s, t):
    """For increasing s and t, count the numbers that appear in both.

    >>> a = Link(3, Link(4, Link(6, Link(7, Link(9, Link(10))))))
    >>> b = Link(1, Link(3, Link(5, Link(7, Link(8)))))
    >>> overlap(a, b)  # 3 and 7
    2
    >>> overlap(a.rest, b)  # just 7
    1
    >>> overlap(Link(0, a), Link(0, b))
    3
    """
    if s is Link.empty or t is Link.empty:
        return 0
    if s.first == t.first:
        return 1 + overlap(s.rest, t.rest)
    elif s.first < t.first:
        return overlap(s.rest, t)
    elif s.first > t.first:
        return overlap(s, t.rest)

def overlap_iterative(s, t):
    """For increasing s and t, count the numbers that appear in both.

    >>> a = Link(3, Link(4, Link(6, Link(7, Link(9, Link(10))))))
    >>> b = Link(1, Link(3, Link(5, Link(7, Link(8)))))
    >>> overlap(a, b)  # 3 and 7
    2
    >>> overlap(a.rest, b)  # just 7
    1
    >>> overlap(Link(0, a), Link(0, b))
    3
    """
    res = 0
    while s is not Link.empty and t is not Link.empty:
        if s.first == t.first:
            res += 1
            s = s.rest
            t = t.rest
        elif s.first < t.first:
            s = s.rest
        else:
            t = t.rest
    return res

Write a function duplicate_link that takes in a linked list s and a value. duplicate_link will mutate s such that if there is a linked list node that has a first equal to value, that node will be duplicated. Note that you should be mutating the original linked list s; you will need to create new Links, but you should not be returning a new linked list.

Note: In order to insert a link into a linked list, you need to modify the .rest of certain links. We encourage you to draw out a doctest to visualize!

Your Answer Run in 61A Code
Solution 
def duplicate_link(s, val):
    """Mutates s so that each element equal to val is followed by another val.

    >>> x = Link(5, Link(4, Link(5)))
    >>> duplicate_link(x, 5)
    >>> x
    Link(5, Link(5, Link(4, Link(5, Link(5)))))
    >>> y = Link(2, Link(4, Link(6, Link(8))))
    >>> duplicate_link(y, 10)
    >>> y
    Link(2, Link(4, Link(6, Link(8))))
    >>> z = Link(1, Link(2, Link(2, Link(3))))
    >>> duplicate_link(z, 2) # ensures that back to back links with val are both duplicated
    >>> z
    Link(1, Link(2, Link(2, Link(2, Link(2, Link(3))))))
    """
    if s is Link.empty:
        return
    elif s.first == val:
        remaining = s.rest
        s.rest = Link(val, remaining)
        duplicate_link(remaining, val)
    else:
        duplicate_link(s.rest, val)

You're done! Excellent work this week. Please be sure to fill out your TA's attendance form to get credit for this discussion!

Extra Challenge

This last question is similar in complexity to an A+ question on an exam. Feel free to skip it, but it's a fun one, so try it if you have time.

Q6: Decimal Expansion

Definition. The decimal expansion of a fraction n/d with n < d is an infinite sequence of digits starting with the 0 before the decimal point and followed by digits that represent the tenths, hundredths, and thousands place (and so on) of the number n/d. E.g., the decimal expansion of 2/3 is a zero followed by an infinite sequence of 6's: 0.6666666....

Implement divide, which takes positive integers n and d with n < d. It returns a linked list with a cycle containing the digits of the infinite decimal expansion of n/d. The provided display function prints the first k digits after the decimal point.

For example, 1/22 would be represented as x below:

>>> 1/22
0.045454545454545456
>>> x = Link(0, Link(0, Link(4, Link(5))))
>>> x.rest.rest.rest.rest = x.rest.rest
>>> display(x, 20)
0.04545454545454545454...
Your Answer
Run in 61A Code
Solution 
def display(s, k=10):
    """Print the first k digits of infinite linked list s as a decimal.

    >>> s = Link(0, Link(8, Link(3)))
    >>> s.rest.rest.rest = s.rest.rest
    >>> display(s)
    0.8333333333...
    """
    assert s.first == 0, f'{s.first} is not 0'
    digits = f'{s.first}.'
    s = s.rest
    for _ in range(k):
        assert s.first >= 0 and s.first < 10, f'{s.first} is not a digit'
        digits += str(s.first)
        s = s.rest
    print(digits + '...')
Your Answer
Run in 61A Code
Solution 
def divide(n, d):
    """Return a linked list with a cycle containing the digits of n/d.

    >>> display(divide(5, 6))
    0.8333333333...
    >>> display(divide(2, 7))
    0.2857142857...
    >>> display(divide(1, 2500))
    0.0004000000...
    >>> display(divide(3, 11))
    0.2727272727...
    >>> display(divide(3, 99))
    0.0303030303...
    >>> display(divide(2, 31), 50)
    0.06451612903225806451612903225806451612903225806451...
    """
    assert n > 0 and n < d
    result = Link(0)  # The zero before the decimal point
    cache = {}
    tail = result
    while n not in cache:
        q, r = 10 * n // d, 10 * n % d
        tail.rest = Link(q)
        tail = tail.rest
        cache[n] = tail
        n = r
    tail.rest = cache[n]
    return result
Place the division pattern from the example above in a while statement: 
>>> q, r = 10 * n // d, 10 * n % d
>>> tail.rest = Link(q)
>>> tail = tail.rest
>>> n = r

While constructing the decimal expansion, store the tail for each n in a dictionary keyed by n. When some n appears a second time, instead of constructing a new Link, set its original link as the rest of the previous link. That will form a cycle of the appropriate length.