Discussion 3: Recursion, Tree Recursion

Getting Started

If you could change one historic event, what would it be? And what would you make happen instead?

Recursion

VERY IMPORTANT: In this discussion, don't check your answers by running your code. Figure things out and check your work by thinking about what your code will do and drawing environment diagrams. Your goal should be to have all checks pass the first time you run them!

A recursive function is a function that calls itself in its body, either directly or indirectly.

Let's look at the canonical example, factorial.

Factorial, denoted with the ! operator, is defined as:

n! = n * (n-1) * ... * 1

For example, 5! = 5 * 4 * 3 * 2 * 1 = 120

The recursive implementation for factorial is as follows:

def factorial(n):
    if n == 0:
        return 1
    return n * factorial(n - 1)

We know from its definition that 0! is 1. Since n == 0 is the smallest number we can compute the factorial of, we use it as our base case. The recursive step also follows from the definition of factorial, i.e., n! = n * (n-1)!.

Recursive functions have three important components:

  1. Base case. You can think of the base case as the case of the simplest function input, or as the stopping condition for the recursion.

    In our example, factorial(0) is our base case for the factorial function.

  2. Recursive call on a smaller problem. You can think of this step as calling the function on a smaller problem that our current problem depends on. We assume that a recursive call on this smaller problem will give us the expected result; we call this idea the "recursive leap of faith".

    In our example, factorial(n) depends on the smaller problem of factorial(n-1).

  3. Solve the larger problem. In step 2, we found the result of a smaller problem. We want to now use that result to figure out what the result of our current problem should be, which is what we want to return from our current function call.

    In our example, we can compute factorial(n) by multiplying the result of our smaller problem factorial(n-1) (which represents (n-1)!) by n (the reasoning being that n! = n * (n-1)!).

The next few questions in lab will have you writing recursive functions. Here are some general tips:

  • Paradoxically, to write a recursive function, you must assume that the function is fully functional before you finish writing it; this is called the recursive leap of faith.
  • Consider how you can solve the current problem using the solution to a simpler version of the problem. The amount of work done in a recursive function can be deceptively little: remember to take the leap of faith and trust the recursion to solve the slightly smaller problem without worrying about how.
  • Think about what the answer would be in the simplest possible case(s). These will be your base cases - the stopping points for your recursive calls. Make sure to consider the possibility that you're missing base cases (this is a common way recursive solutions fail).
  • It may help to write an iterative version first.

Q1: Warm Up: Recursive Multiplication

These exercises are meant to help refresh your memory of the topics covered in lecture.

Write a function that takes two numbers m and n and returns their product. Assume m and n are positive integers. Use recursion, not mul or *.

Hint: 5 * 3 = 5 + (5 * 2) = 5 + 5 + (5 * 1).

For the base case, what is the simplest possible input for multiply?

If one of the inputs is one, you simply return the other input.

For the recursive case, what are we doing in every step? How do we change m or n to make this a smaller version of the same problem?

The first call will calculate a value that is n less than the total, while the second will calculate a value that is m less. Either recursive call will work, but only multiply(m, n - 1) is used in this solution.

Your Answer
Run in 61A Code
Solution 
def multiply(m, n):
    """Takes two positive integers and returns their product using recursion.
    >>> multiply(5, 3)
    15
    """
    if n == 1:
        return m
    else:
        return m + multiply(m, n - 1)

Q2: Swipe

Implement swipe, which prints the digits of argument n, one per line, first backward then forward. The left-most digit is printed only once. Do not use while or for or str. (Use recursion, of course!)

Your Answer
Run in 61A Code
Solution 
def swipe(n):
    """Print the digits of n, one per line, first backward then forward.

    >>> swipe(2837)
    7
    3
    8
    2
    8
    3
    7
    """
    if n < 10:
        print(n)
    else:
        print(n % 10)
        swipe(n // 10)
        print(n % 10)

Q3: Skip Factorial

Define the base case for the skip_factorial function, which returns the product of every other positive integer, starting with n.

Your Answer
Run in 61A Code
Solution 
def skip_factorial(n):
    """Return the product of positive integers n * (n - 2) * (n - 4) * ...

    >>> skip_factorial(5) # 5 * 3 * 1
    15
    >>> skip_factorial(8) # 8 * 6 * 4 * 2
    384
    """
    if n <= 2:
        return n
    else:
        return n * skip_factorial(n - 2)

Q4: Recursive Hailstone

Recall the hailstone function from Homework 1. First, pick a positive integer n as the start. If n is even, divide it by 2. If n is odd, multiply it by 3 and add 1. Repeat this process until n is 1. Complete this recursive version of hailstone that prints out the values of the sequence and returns the number of steps.

Your Answer
Run in 61A Code
Solution 
def hailstone(n):
    """Print out the hailstone sequence starting at n, 
    and return the number of elements in the sequence.
    >>> a = hailstone(10)
    10
    5
    16
    8
    4
    2
    1
    >>> a
    7
    >>> b = hailstone(1)
    1
    >>> b
    1
    """
    print(n)
    if n % 2 == 0:
        return even(n)
    else:
        return odd(n)

def even(n):
    return 1 + hailstone(n // 2)

def odd(n):
    if n == 1:
        return 1
    else:
        return 1 + hailstone(3 * n + 1)

Tree Recursion

A tree recursive function is a recursive function that makes more than one call to itself, resulting in a tree-like series of calls.

For example, this is the Virahanka-Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, ....

Each term is the sum of the previous two terms. This tree-recursive function calculates the nth Virahanka-Fibonacci number.

def virfib(n):
    if n == 0 or n == 1:
        return n
    return virfib(n - 1) + virfib(n - 2)

Calling virfib(6) results in a call structure that resembles an upside-down tree (where f is virfib):

Virahanka-Fibonacci tree.

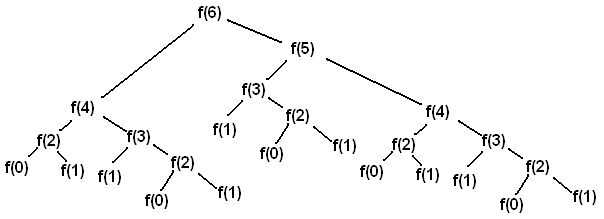
Each recursive call f(i) makes a call to f(i-1) and a call to f(i-2). Whenever we reach an f(0) or f(1) call, we can directly return 0 or 1 without making more recursive calls. These calls are our base cases.

A base case returns an answer without depending on the results of other calls. Once we reach a base case, we can go back and answer the recursive calls that led to the base case.

As we will see, tree recursion is often effective for problems with branching choices. In these problems, you make a recursive call for each branching choice.

Q5: Count Stair Ways

Imagine that you want to go up a flight of stairs that has n steps, where n is a positive integer. You can take either one or two steps each time you move. In how many ways can you go up the entire flight of stairs?

You'll write a function count_stair_ways to answer this question. Before you write any code, consider:

  • How many ways are there to go up a flight of stairs with n = 1 step? What about n = 2 steps? Try writing or drawing out some other examples and see if you notice any patterns.

Solution: When there is only one step, there is only one way to go up. When there are two steps, we can go up in two ways: take a single 2-step, or take two 1-steps.

  • What is the base case for this question? What is the smallest input?

Solution: We actually have two base cases! Our first base case is when there is one step left. n = 1 is the smallest input because 1 is the smallest positive integer.

Our second base case is when there are two steps left. The primary solution (found below) cannot solve count_stair_ways(2) recursively because count_stair_ways(0) is undefined.

(virfib has two base cases for a similar reason: virfib(1) cannot be solved recursively because virfib(-1) is undefined.)

Alternate solution: Our first base case is when there are no steps left. This means we reached the top of the stairs with our last action.

Our second base case is when we have overstepped. This means our last action was invalid; in other words, we took two steps when only one step remained.

Solution: count_stair_ways(n - 1) is the number of ways to go up n - 1 stairs. Equivalently, count_stair_ways(n - 1) is the number of ways to go up n stairs if our first action is taking one step.

count_stair_ways(n - 2) is the number of ways to go up n - 2 stairs. Equivalently, count_stair_ways(n - 2) is the number of ways to go up n stairs if our first action is taking two steps.

Now, fill in the code for count_stair_ways:

Your Answer
Run in 61A Code
Solution 
def count_stair_ways(n):
    """Returns the number of ways to climb up a flight of
    n stairs, moving either one step or two steps at a time.
    >>> count_stair_ways(1)
    1
    >>> count_stair_ways(2)
    2
    >>> count_stair_ways(4)
    5
    """
    if n == 1:
        return 1
    elif n == 2:
        return 2
    return count_stair_ways(n-1) + count_stair_ways(n-2)
Here's an alternate solution that corresponds to the alternate base cases: 
def count_stair_ways_alt(n):
    """Returns the number of ways to climb up a flight of
    n stairs, moving either 1 step or 2 steps at a time.
    >>> count_stair_ways_alt(4)
    5
    """
    if n == 0:
        return 1
    elif n < 0:
        return 0
    return count_stair_ways_alt(n-1) + count_stair_ways_alt(n-2)

You can use Recursion Visualizer to step through the call structure of count_stair_ways(4) for the primary solution.

You're done! Excellent work this week. Please be sure to fill out your TA's attendance form to get credit for this discussion!

Extra Challenge

Try these out if you like challenges. You might have fun.

Q6: Subsequences

A subsequence of a sequence S is a subset of elements from S, in the same order they appear in S. Consider the list [1, 2, 3]. Here are a few of its subsequences [], [1, 3], [2], and [1, 2, 3].

Write a function that takes in a list and returns all possible subsequences of that list. The subsequences should be returned as a list of lists, where each nested list is a subsequence of the original input.

In order to accomplish this, you might first want to write a function insert_into_all that takes an item and a list of lists, adds the item to the beginning of each nested list, and returns the resulting list.

Your Answer
Run in 61A Code
Solution 
def insert_into_all(item, nested_list):
    """Return a new list consisting of all the lists in nested_list,
    but with item added to the front of each. You can assume that
    nested_list is a list of lists.

    >>> nl = [[], [1, 2], [3]]
    >>> insert_into_all(0, nl)
    [[0], [0, 1, 2], [0, 3]]
    """
    return [[item] + lst for lst in nested_list]

def subseqs(s):
    """Return a nested list (a list of lists) of all subsequences of S.
    The subsequences can appear in any order. You can assume S is a list.

    >>> seqs = subseqs([1, 2, 3])
    >>> sorted(seqs)
    [[], [1], [1, 2], [1, 2, 3], [1, 3], [2], [2, 3], [3]]
    >>> subseqs([])
    [[]]
    """
    if not s:
        return [[]]
    else:
        subset = subseqs(s[1:])
        return insert_into_all(s[0], subset) + subset